Научно-методические аспекты изучения курса
Научно-методические аспекты изучения курса
Изучение информатики в начальной школе
В сознании современных людей слово информатика неразрывно связано со словом компьютер. Многим кажется, что изучать информатику без компьютера – это как учиться ездить на велосипеде без велосипеда. Это и верно, и неверно. Есть наука информатика, некоторым разделам которой и посвящен настоящий курс, а есть информационные технологии и информационная культура и т. д. Часто и то и другое называется информатикой. Современные информационные технологии в значительной степени опираются на использование компьютера. В этом смысле информатика и компьютер неразделимы. Верно и то, что очень многие информационные технологии без компьютера изучать не стоит. Известно также, что многие задачи и результаты современной теоретической информатики возникли в связи с использованием компьютеров в нашей жизни.
Однако важность теоретической информатики как науки выходит за рамки изучения компьютеров. Наиболее значительные ее результаты, относящиеся к математике мышления и коммуникации, были получены в конце XIX – первой половине XX в., до появления компьютеров и их вхождения в нашу жизнь. Среди ученых-математиков и философов, внесших существенный вклад в информатику, есть и зарубежные – Г. Фреге, Д. Гильберт, К. Гедель, А. Тьюринг, Н. Винер, и российские – А. Н. Колмогоров, А. И. Мальцев, А. А. Марков.
Итак, в силу изложенных выше обстоятельств курс информатики можно и, как нам кажется, нужно изучать, даже если в вашей школе нет ни одного компьютера. Полезны ли полученные при этом знания будущему пользователю компьютеров и других средств информационных технологий? Мы уверены, что да.
Полезен ли наш курс, если параллельно ваш класс имеет возможность работать на компьютерах? Да, и мы предлагаем вам курс, объединяющий информатику и информационные технологии. Данный курс не только интегрирует теоретическую информатику и информационные технологии, но и дает учащимся навыки использования компьютера и другие информационно-технологические навыки, которые могут (и должны) немедленно применяться учащимися при изучении различных предметов.
Мы считаем (и будем иллюстрировать это в дальнейшем), что изучение данного курса параллельно с основными курсами начального образования позволяет существенно повысить качество изучения традиционных тем в этих курсах за счет формирования у учащихся еще одной, «информатической» точки зрения и развития их мыслительных и коммуникативных способностей. Мы рекомендуем вам не забывать об этой перспективе и, если вы преподаете одновременно информатику и эти основные курсы, постоянно обращать внимание на возможные связи.
Главная цель изучения курса информатики – формирование у ребенка информационной культуры, под которой мы понимаем систему общих умений практически работать с информацией и передавать ее другим. Жизнь требует, чтобы многие элементы информационной культуры вошли в начальное образование – в школе и дома. К информационной культуре относится умение пользоваться источниками информации – справочниками, словарями, энциклопедиями, расписанием поездов и программой телевизионных передач и др. К ней же можно отнести и умение вести телефонный разговор, и умение смотреть (и не смотреть) телевизор, и умение записать свой адрес и вести записную книжку. В нашем курсе учащиеся усваивают ряд фундаментальных понятий, лежащих в основе информационной культуры и необязательно связанных с компьютером.
Математика как игра
Сравнение математики с игрой по формальным правилам и построение философии математики на этой основе принадлежит Давиду Гильберту, одному из крупнейших математиков конца XIX – начала XX века. Это сравнение весьма важно для нас, мы его уже упоминали в этой книге и будем к нему еще возвращаться. В информатическом контексте такое сравнение особенно плодотворно – конечно, не в связи с компьютерными играми, а в связи с общим стилем взаимодействия человека с компьютером, когда компьютер действует по правилам, не воспринимая обширного и не всегда четкого контекста (окружения), в котором живет человек.
Одной из важных для нас особенностей игры является то, что создатели курса – математики и лингвисты, учителя и дети, работающие с учебником, – все играют по одним и тем же правилам – правилам математики и информатики. Гроссмейстер выигрывает партию у любителя не потому, что его «назначили» гроссмейстером, – правда в шахматах для всех одна.
Организация работы на уроке
Авторские идеи, заложенные в основу курса, требуют несколько необычной для начальной школы организации урока. Мы уверены в необходимости дать ученикам свободу самостоятельной работы, самостоятельного исследования. Это позволит детям учиться и развивать свои способности более охотно и эффективно, чем при традиционной форме проведения уроков.
Предлагаемая модель урока – это самостоятельная работа учащегося с учебником, самостоятельное изучение им листов определений и дальнейшее решение задач. Учителю отводится роль консультанта в сложных ситуациях и организатора обсуждений, как индивидуальных, так и групповых. Обсуждения чаще всего проводятся по окончании решения задач для того, чтобы ученики могли поделиться своими идеями и способами решения задач, чтобы ребята учились оформлять свои мысли вербально (словесно), чтобы обобщить опыт, накопленный ребятами в ходе решения задач. Такая модель урока поддерживается спецификой учебника, который содержит полную информацию для решения любой задачи.
Мы считаем вполне допустимым, если в некоторых случаях ученики сами будут выбирать, какую задачу решать, однако их свобода все-таки будет ограничена, во-первых, последовательностью изложения материала, во-вторых, объемом обязательных знаний и умений по данному предмету, которыми в результате изучения курса должен обладать каждый ученик. Исходя из этих ограничений, мы советуем вам придерживаться следующих правил при планировании урока. На каждом уроке все учащиеся работают с одним и тем же листом определений (это они не могут выбирать). Листы определений необходимо проходить в том же порядке, в котором они приведены в учебнике, ничего не пропуская, даже если вам кажется, что информация, изложенная там, ребятам знакома. В учебнике помечены задачи, входящие в обязательный минимум, их необходимо решить каждому учащемуся для качественного усвоения материала курса (это задачи, помеченные как обязательные). В обязательные задачи входят не только упражнения на текущий лист определения, но и некоторые задачи на повторение, поскольку текущее повторение является одной из важных идей построения курса.
В учебнике также довольно много необязательных задач. Они помогут вам организовать урок не только продуктивно, но и интересно, а также осуществить дифференцированный подход к каждому ученику. Среди необязательных задач есть задачи на повторение тем различных листов определений, причем разной степени сложности, которые позволят проводить текущее повторение, опираясь на уровень и специфику детей. Также среди этих задач можно легко найти материал для текущего контроля – самостоятельных и проверочных работ. Наконец, среди необязательных задач встречаются довольно трудные, которые помогут не просто занять сильного ученика, но позволят ему реализовать свои способности и продвинуться на пути к новым вершинам.
Обратите внимание на то, что есть задачи трудные технически (например, если в задании очень много объектов), а есть задачи, трудные содержательно. Таким образом, при подготовке к уроку надо внимательно изучить необязательные задачи и решить, как использовать их наиболее эффективно. Ну и, конечно, не стоит стремиться к тому, чтобы все дети решили все необязательные задачи.
Домашние задания
Содержание курса может быть изучено без домашних заданий. Однако, если вы заметите, что класс медлительный и большинство ребят систематически не справляются с объемом обязательных задач, либо дети и родители будут этого требовать, можно разрешить выполнение заданий дома. В этом случае вам, возможно, придется столкнуться с множеством вопросов родителей. Постарайтесь сделать это обсуждение приятным для обеих сторон. Один из способов – предложить родителям побеседовать друг с другом. Вы можете дать им почитать книгу для учителя, предложить самим порешать детские задачи (систематически, подряд, начиная с самой первой!). Другой способ – постараться объяснить родителям, что очень важно, чтобы ребенок работал с учебником самостоятельно даже дома – помощь родителей может состоять лишь в поддержке и обсуждении неясных вопросов, но, ни в коем случае не в подсказке.
Ключевые слова и выражения
Одна из основных задач курса, над которым мы с вами работаем, как и всего обучения в школе, – это усвоение языка. В ходе работы над курсом мы постепенно вводим ключевые слова и выражения, которые важны для нас потому, что мы систематически используем их в наших текстах, причем с точно определенным и фиксированным смыслом, понятным и одинаковым для всех детей и учителя.
Словарь ключевых слов курса состоит из слов русского языка (таких, например, как «буква») и выражений (таких, например, как «Раскрась картинку как хочешь»). Поначалу это слова, которые ребенок уже слышал, хотя их значение может до некоторой степени отличаться от уже сформировавшегося у ребенка. Позднее появляются и новые для него слова. Для всех ключевых слов мы стараемся максимально подробно и ясно для ребенка (а также для учителя и родителей) разъяснить, проиллюстрировать и зафиксировать их смысл. Очень важно, чтобы относительно каждого слова этого словаря у нас с детьми было фиксированное и одинаковое понимание, что это слово значит. Некоторые ключевые слова вводятся непосредственно в задачах учебника. В таких случаях это обязательно отмечено в комментарии к данной задаче.
Способ определений понятий в нашем курсе
Вы, наверняка заметили, что в нашем курсе почти нет формальных определений. Также в курсе сравнительно немного абстрактных объяснений и описаний. Для взрослого такие пояснения и описания могут оказаться полезным, для ребенка – вряд ли. Похожая ситуация возникает во многих курсах и учебниках, где ребенку предлагается выучить наизусть определение, мало что добавляющее к демонстрации учителем набора примеров и не способствующее пониманию материала. Наш подход состоит в перемещении центра тяжести с недостаточно информативных определений на примеры.
При этом мы используем естественную способность ребенка к классификации. Никто не пытается дать ребенку определение того, что такое собака, но он легко в трехлетнем возрасте отличит собаку от кошки. Так же и в нашей ситуации: большинство понятий курса формируется на примерах. Конечно, мы следим за тем, чтобы наши понятия и формирующие их листы определений сводили до минимума возможность неоднозначного (двусмысленного) понимания. Совсем исключить потенциальную возможность двусмысленности, если даешь определение на примерах, нельзя. Поэтому, обсуждая ту или иную задачу с детьми, вы можете прибегнуть к словесным формулировкам тех или иных понятий. Важно только, чтобы эти словесные формулировки воспринимались как вспомогательные и ни в коем случае не заучивались наизусть.
Область одной задачи
В учебнике почти на каждой странице имеется не одна, а несколько задач. Отделить одну от другой нам с вами достаточно легко. Помимо текста задания, есть также поле, где расположены объекты, к которым относится задание. На первых порах это, прежде всего, картинки, фигурки, бусины и т. п. Эта часть страницы – «позиция в игре» или «микромир», где станет сейчас развиваться действие, в котором вы с ребенком будете жить несколько минут. Кроме этого, к полю задачи может относиться еще и лист вырезания. Для взрослого нетрудно определить, какое поле, к какой задаче относится. Однако то, что вся часть страницы, скажем, от номера 1 до номера 2 – это один цельный объект, содержащий и правила игры, и начальную позицию, иногда может быть не очевидным для ребенка. Умение отвлечься от остального содержания страницы, от других страниц и вообще от всего окружающего и сосредоточиться на условии задачи и ее микромире – важная способность. Старайтесь развивать ее у детей с первых уроков, ведь, как и в случае с правилами игры, здесь тоже формируются у учащегося как навыки работы с информатическими понятиями, так и общие жизненные умения.
Ситуации недетерминированного выбора
Очень важным и, возможно, необычным для вас является использование на листах определений и в задачах курса ситуаций недетерминированного выбора, соответствующих выражениям: каким хочешь, сколько хочешь, как хочешь. Важность таких ситуаций связана со следующим принципом:
Мы стараемся как можно более ясно и явно формулировать все условия и ограничения каждой задачи. Суждение о том, правильно решена задача или нет, в равной степени должно быть доступно и ребенку, и учителю.
Частной ситуацией, в которой подчеркнуто используется этот принцип, и является выражение «как хочешь» и подобные. Так, если в задании написано «Раскрась какими хочешь цветами», значит ребенок может выбирать абсолютно любые цвета и набора введенных цветов, в том числе он может все области картинки раскрасить черным. Даже если получается некрасиво, необходимо похвалить ребенка – он должен понимать, что решил задачу правильно. Если в задании написано «Нарисуй сколько хочешь», ребенок может нарисовать любое число объектов, в том числе и нуль.
С точки зрения методологии изучения информатики и математики, правильного их использования и творческой работы в этих науках важным является умение привести произвольный пример, удовлетворяющий данному определению: «А почему бы нам не попробовать взять произвольную...» В целом умение действовать и планировать действия в системе ограничений и в отсутствие ограничений очень важно в работе с информационными системами, например в программировании. Вы понимаете, что это умение полезно и в чисто житейских ситуациях, где бывает нужно дать волю своей фантазии, даже капризу, или попытаться угадать, на каком пути повезет.
С научной точки зрения операция произвольного (недетерминированного) выбора является одной из простейших и фундаментальнейших при описании процессов в теории алгоритмов.
Дискретизация
В курсе будет встречаться много задач на клетчатой бумаге. Такие задачи бывают связаны с одним из важных понятий информатики – дискретизацией. Это понятие описывает ситуацию, когда имеется какой-то объект, например геометрическая фигура, или изображение, или звук, а мы хотим его описать более или менее точно с помощью цепочки букв и знаков – текста. Делать это можно по-разному. Можно сказать: «Вот тут, в углу, квадрат, а рядом что-то похожее на ухо». А можно разбить изображение на квадратики и перечислить подряд цвета квадратиков. Конечно, на границе цветов возникнет проблема: какого цвета там квадратик? Придется тем не менее выбрать какой-нибудь один цвет. Поэтому-то описание и становится приближенным.
В жизни мы сталкиваемся с такой ситуацией довольно часто; например, мы измеряем что-то сантиметром и говорим: длина стола 108 см, а на самом деле она чуть больше – 108,1429… см. 108 – это приближение, дискретизация длины стола.
Мы вышиваем крестиком картинку, переведенную по клеткам. Это дискретизация, и картинка получается дискретной. На экране телевизора изображение создается дискретными элементами. Дискретное (иногда говорят: оцифрованное, цифровое) представление информации становится все более и более распространенным.
Вероятно, вы знаете, что любое изображение на экране компьютера именно такое – дискретное, составленное из мелких элементов. Эти элементы могут быть настолько мелкими, что человеческий глаз их не различает. Мы приводим здесь примеры компьютерных картинок – слева с совсем маленькими, а справа с довольно большими элементами. Посмотрите на правые картинки с расстояния 3 метров – дискретизация «исчезает»!

Самой чистой записью звука считается цифровая, дискретизованная; появляются цифровые (digital) фотоаппараты и видеокамеры и т. д. Книга одного из лидеров современной информационной технологии, директора Медиалаборатории Массачусетского технологического института Николаса Негропонте (Nicolas Negroponte) называется «Being Digital» (примерный перевод: «Быть дискретным (компьютерным)»).
Логические предикаты: все, каждый
Мы надеемся, что вам и вашим ученикам понятия все/каждый покажутся простыми. Они и на самом деле простые («каждый его знает»). Однако не всегда это было так. Вы, наверное, слышали о силлогизмах Аристотеля. Их постижение составляло существенную часть средневекового высшего образования. Возможно, вы встречали и примеры силлогизмов вроде:
Все люди смертны.
Сократ – человек.
_______________________________________
Следовательно, Сократ смертен.
Мы надеемся, что ваши ученики без труда будут в будущем строить рассуждения такого рода. Но мы предостерегаем вас от игнорирования того, что понимание детьми таких «очевидных» слов, как, например, каждый, поначалу может немного или даже существенно отличаться от вашего.
Слова «все», «каждый» всегда относятся к некоторой совокупности объектов. Иногда эта совокупность устроена сложно – все атомы во Вселенной или все действительные числа. Мы, однако, довольно долго будем иметь дело с простыми совокупностями, умещающимися на одной странице, где объекты сравнительно легко перебрать по одному.
Именно такой перебор (по одному) и нужно осуществлять каждый раз, когда мы выполняем какое-то действие или проверяем какое-то свойство для всех объектов. Не надо формулировать это в виде правила. Лучше, если дети будут относиться к словам все, каждый просто как к словам русского языка с очевидным смыслом. Однако желательно проверить, все ли дети (опять все!) правильно понимают этот смысл и действительно в какой-то мере систематически просматривают все объекты. Это очень важно для формирования информатического, конструктивного взгляда на понятия и процессы.
Метод полного перебора
Как вы знаете, в нашем курсе мы стараемся сделать наглядными, видимыми объекты информатики (а также математики и лингвистики), так же как и отношения между ними и действия над ними. Такая визуализация объектов информатики, сочетание образного и символического описаний очень продуктивны в обучении. Они же являются одним из основных направлений развития информационных технологий в целом и их применения в образовании в частности. Все чаще и чаще, рассказывая что-то друг другу, люди одновременно показывают это на экране, куда проецируется компьютерное изображение, где появляются все необходимые иллюстрации. Графическая насыщенность курса требует формирования некоторых специфических навыков (полезных, конечно, и вне курса).
Сейчас речь пойдет об одном важном умении: просматривать и сортировать графические или символьные объекты, расположенные в некотором поле (скажем, на странице или в поле одной задачи). В жизни такое умение необходимо везде, начиная от чтения меню и расписания движения поездов и самолетов, чтения географических карт и заканчивая поиском подходящих туфель на полке магазина.
Процедура просмотра, которую обычно использует ребенок, а часто и взрослый, хаотическая. Это – беспорядочное перескакивание с одного предмета на другой. Иногда эта стратегия не так уж плоха. Однако она не нужна в случаях, когда требуется действительно полный просмотр, или, как иногда говорят в информатике и математике, полный перебор. Поэтому необходимо вычеркивать или обводить уже просмотренный объект или хотя бы ставить на нем (или вблизи его) точку. Не надо запрещать детям делать это. (Конечно, можно посоветовать им, например, ограничиться точкой вместо вычеркивания.) Но если ребенок не использует графических пометок, перечисленных выше, полезно предложить ему некоторую стратегию просмотра. (Пример стратегии – просматривать объекты в ряду слева направо, переходя к следующему ряду сверху вниз.) На первых порах использование этой стратегии можно облегчить с помощью линейки, которую надо перемещать сверху вниз, каждый раз просматривая появившиеся целиком над линейкой объекты. Конечно, эта стратегия требует большой аккуратности и хорошо работает, если объекты расположены по строкам.
Через несколько лет на уроках информатики детям придется составлять программы для компьютера, включающие полный просмотр, сортировку объектов и другие важные операции. Мы хотели бы, чтобы дети уже хорошо понимали, что это значит, и умели бы это делать вручную. Иначе как они смогут сознательно обучить этому компьютер?
Метод разбиения задачи на подзадачи
В проекте «Разделяй и властвуй» дети используют метод разбиения задачи на подзадачи. Теперь для тех, кому небезразличны философские аспекты нашего проекта, мы предлагаем несколько тем для размышления.
Многие первобытные космогонические мифы начинаются с разделения (дотоле слитных) Божественных Супругов (Земли и Неба, Тьмы и Света, Ночи и Дня). В более поздней и, так сказать, рационализированной мифологии античности происходит разделение и последующее упорядочение Хаоса.
Разделенные части образуют вначале двоичное противопоставление (бинарную оппозицию), позже появляются деления с более высокой кратностью. Общее здесь то, что во всех случаях разделенным частям даются имена, позволяющие человеку более уверенно ориентироваться в окружающем его мире, приспосабливаться к окружающей среде, а затем властвовать над ней и преобразовывать ее соответственно своим представлениям о должном, истинном и прекрасном. Именование предметов и выявление значения сложных имен – одна из важнейших частей нашего курса, с которой мы вскоре встретимся.
Согласно религиозным верованиям иудеев и христиан Небо и Земля – не результат разделения (и формовки) какой-то прежде бывшей субстанции, а нечто, творимое из ничего. Это не космогония, а космопоэзис. Но разделение, ведущее к Властвованию через Номинацию (присвоение имени), имеет место и там, хотя и несколько позже.
Разделение сущего на роды и виды, их Именование и Властвование над ними оказываются тесно сопряженными моментами всей последующей истории европейской мысли и практики.
Вплоть до наших дней философы и логики неустанно обсуждают проблему разделения целого – по каким «линиям» и на какие части его членить и как устанавливать неделимые далее единицы членения. Большое внимание уделяют этому и современные лингвисты. Так, школа Сэпира-Уорфа утверждает, что человек членит в своем сознании (а далее и в материальной деятельности) внешний мир именно таким образом, каким это подсказывает ему его язык.
В античной натурфилософии, предшествовавшей физике и химии, стремление разделять представление о данной (любой) вещи на все более мелкие части, чтобы узнать, «как они устроены», т. е. сделать их прежде всего в мысли подвластными нашему разуму, приводит к теории атомизма. (Надо ли напоминать, сколь огромную, грозную и опасную власть над силами природы дала человеку эта теория в ходе своего развития?)
Атомы, однако, без-качественны, у них нет индивидуальности, они не различимы друг от друга и не имеют имен. Поэтому приходится мыслить различные сочетания атомов («элементы»), обладающие различимыми свойствами и хотя бы «видовой» индивидуальностью и именами.
У Лейбница индивидуальное, или особенное, позволяющее различать (или отождествлять) два объекта, заключается в совокупности качеств каждого из них. Когда же все качества данного объекта перечислены, его особенность точно определена. Слова, обозначающие качества (их совокупности), можно считать «именами» объектов, у которых эти качества обнаруживаются. В нашем курсе, например, мы сталкиваемся с классификацией простейших объектов – бусин – по форме и цвету.
До сих пор мы рассматривали разделение, номинацию и властвование в аспекте «естественного» – так, как оно уже есть, как дано нам природой (или Богом). Скажем пару слов и об «искусственном».
Начнем с политики: правители Древнего Рима, превращая завоеванные ими земли в провинции, руководствовались принципом «divide et impera», т. е. «разделяй и властвуй». Жители покоренных областей обязаны были платить столице большую дань, подвергались нещадной эксплуатации и при малейшей возможности готовы были восстать против римлян. Но часть провинциальных городов и общин получали свободу от налогов и назывались «свободными». Они чрезвычайно дорожили своими привилегиями и служили Риму верной опорой при усмирении непокорных.
Разделение как условие властвования над чем-то нам данным нагляднее всего предстает в технологии. Большое количество вещества (глины, дерева, камня, металла) трудно или практически невозможно обрабатывать. Мастеру (первоначальное значение слова «мастер» – «хозяин» или «владыка») нужно сперва разделить материал на небольшие части, легко поддающиеся обработке, из которых потом можно изготавливать отдельные детали, а затем собирать и соединять их в крупные конструкции (составные орудия, механизмы, машины и системы машин), естественным путем не возникающие.
В мире современной информационной технологии тот же принцип является наиболее универсальным приемом при поиске и обработке информации.
Ряд философских соображений, приведенных выше в сконденсированном виде, будет далее развит в нашем курсе более детально и наглядно. Здесь мы привели их, скорее, чтобы дать вам почувствовать перспективу, пусть даже теряющуюся в дымке высоких материй.
Число областей. Топология
Число областей в картинке относится числу топологических свойств. Математику часто определяли как науку о числах и фигурах. В современной математике роль чисел существенно меньше, как и роль фигур в их классическом понимании. Эти изменения находят отражение в нашем курсе: в нем, в частности, появляются начала топологии – важной и интересной области современной математики. Особое значение топология приобретает в связи с развитием информатики, начиная с проблем топологии интегральных схем и кончая задачами распознавания изображений компьютером.
Чтобы пояснить, чем занимается топология, можно сказать, что она изучает свойства фигур в пространстве, которые сохраняются при непрерывных преобразованиях этого пространства. Но это лишь приблизительное описание, в частности, потому, что математическое понимание пространства тоже не совпадает с нашим обычным пониманием и требует особого пояснения. Сделаем это на следующем примере.
Давайте выберем в качестве пространства воздушный шар, только абстрактный, математический: его можно как угодно растягивать, сжимать, деформировать без всякого сохранения размеров, но не прорывать. Нарисуем на шаре какую-нибудь кривую, опять-таки «абстрактным», математическим пером: у этой кривой нет никакой толщины. Может случиться, что она разобьет шар на две области так, что в каждой из этих областей можно будет перейти от одной произвольной точки к любой другой, не пересекая нашу кривую.
Вот пример такой кривой на шаре:
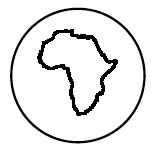
А вот примеры кривых на шаре, для которых рассматриваемое нами свойство не выполнено:
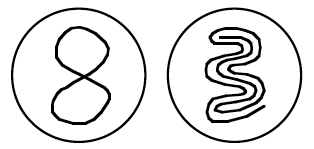
Итак, мы описали свойство кривой на шаре. (Точнее, как сказали бы математики, на сфере, потому что для математиков шар – это заполненная сфера.)
Вполне похоже, что обсуждаемое нами свойство является топологическим. Это значит, что если кривая разбивала сферу на две области и мы сферу как-то деформировали, то деформированная кривая будет опять разбивать деформированную сферу на две области.
И действительно, если соответствующим (и естественным) образом определить все используемые математические понятия, то получится математическое определение топологического свойства, отвечающее нашим интуитивным представлениям.
Многие понятия топологии, обладая формальными математическими определениями, имеют весьма ясное интуитивное содержание. Более того, это содержание иногда относится к базовым понятиям, описывающим окружающий нас мир. Поэтому некоторые из этих понятий довольно часто появляются в курсах разных авторов – в учебниках и рабочих тетрадях для первого класса. Для нас задачи, включающие такой материал, являются частью начал образования, и заложенные в них идеи получают развитие на протяжении всего курса.
Кстати, приведем пример свойства, не являющегося топологическим: «Кривая ограничивает область, имеющую площадь 4 см 2».
Именование объектов
Присвоение имен – важнейшая функция человеческого мышления и языка. Согласно Священному Писанию еще до сотворения Евы первому человеку было предоставлено право назвать сотворенных Господом животных и птиц:
«Господь Бог образовал из земли всех животных полевых и всех птиц поднебесных и привел их к человеку, чтобы видеть, как он назовет их, и чтобы, как наречет человек всякую душу живую, так и было имя ей».
Замечательный русский поэт второй половины ХХ века Давид Самойлов писал:
У зим бывают имена.
Одна из них звалась Наталья.
И были в ней молчанья тайна,
И холод, и голубизна...
Понятие имени – одно из важнейших в информатике и математике. Мы в нашем курсе будем давать имена самым разным объектам: цепочкам, фигуркам и пр. Именем может быть любое слово (вспомните наше определение слова как любой цепочки букв) и даже любая цепочка букв и цифр.
В традиционных книгах по информатике и математике часто говорят не об именах и значениях, а о переменных, параметрах, константах и их значениях. Несколько огрубляя ситуацию, можно сказать, что переменные меняют значение часто и их значение во многих случаях неизвестно (вот еще одно слово традиционной математики – «неизвестное», мы же употребляем слово «неизвестно» в более обычном смысле). Параметры более постоянны в своих значениях; впрочем, эти значения тоже нам обычно неизвестны. Что касается констант, то обычно (но не всегда) их значения действительно постоянны и в общем-то известны, например число p. Вы видите, что ситуация не такая простая, и поэтому мы в начальной школе предпочитаем говорить только об именах.
Часто в математике и особенно в информатике используются имена, не просто являющиеся произвольными цепочками букв, но и отражающие использование этих имен: «подлежащее», «время в пути» и т. п.
Сокращения и «вольности речи»
В повседневной жизни люди часто произносят фразы и пишут тексты, которые могут быть поняты по-разному, причем иногда разница в понимании может оказаться весьма существенной. Как правило, в таких случаях имеются обстоятельства, которые помогают слушающему или читающему выбрать из различных пониманий то, которое имеется в виду говорящим или пишущим. Если же уверенности нет, то можно задать уточняющий вопрос, спросить, что имеет в виду собеседник. В случае письменного текста можно попытаться перечитать еще раз предшествующий фрагмент или продолжить чтение, рассчитывая на прояснение в дальнейшем.
Причин возникновения неоднозначности в тексте много. Одна из них – стремление к краткости. Полный текст был бы слишком длинным, и говорящий надеется, что его поймут с полуслова.
В математике тексты, в особенности записанные на специально придуманных языках математических формул, чаще оказываются однозначными, и в данном случае это является важным. Однако и здесь, особенно в неформальной части математических текстов, возникают неоднозначности, но математики заведомо идут на это ради большей краткости и понятности всего текста. Дело в том, что нередко, чтобы достичь однозначности понимания текста и полной точности выражений, приходится делать его очень длинным и громоздким, а значит, трудным для восприятия. Однако при работе с компьютером это часто является необходимым. Возникает проблема: компьютер требует полной однозначности, а человек – если не лаконичности, то по крайней мере обозримости.
Мы уже понимаем, что значат слова «цепочка с именем Х» или «фигурка с именем А». Как мы уже показали, можно говорить и короче – цепочка Х и фигурка А. Проблема возникает в связи с тем, что имена у нас тоже цепочки. Поэтому, когда мы будем говорить «цепочка Х», нам придется догадываться, идет ли речь о цепочке из одной бусины Х или о какой-то другой цепочке с именем Х, может быть, состоящей из тысячи бусин. Иногда догадаться будет просто невозможно, и тогда нам придется возвращаться к более точному и более громоздкому выражению «цепочка с именем Х».
Трудные задачи
Вы, вероятно, уже заметили, что в нашем учебнике имеется несколько задач, существенно более трудных, чем остальные. Они всегда необязательные. Какая же от них польза?
В вашем классе наверняка найдутся дети, которые быстро решат все остальные задачи. Можно после этого занять их другими делами, но достаточно естественно занять их решением трудной задачи. Трудность и радость преодоления материала – одно из важных учебных, интеллектуальных и вообще жизненных ощущений, с которым мы хотим познакомить детей.
Некоторые дети могут обладать какими-то специфическими способностями и не так уж быстро решать задачи курса. Но как раз трудная задача у них получится. Это может послужить как основой для самоутверждения такого ученика, так и способом открытия в нем неординарных способностей.
Работая с якутскими учителями, мы обнаружили, что почти все они решают задачи графического характера значительно быстрее московских, хотя в решении других задач находятся на обычном «московском» уровне. Потом оказалось, что аналогичные наблюдения уже были сделаны психологами до нас.
Неудавшаяся попытка решить трудную задачу может быть полезна для того, чтобы продемонстрировать ученику (и нам с вами), что, даже оперируя с очень простыми базовыми понятиями, мы можем столкнуться с весьма сложными вопросами. Достаточно интересно каждый раз подумать, с чем же связана сложность.
Попробуйте заранее обдумать упрощенные варианты каждой из трудных задач; их вы сможете предложить тем ученикам, которые заинтересовались этой задачей, но не смогли ее решить самостоятельно. Желательно, чтобы ваша помощь не носила характера прямой подсказки – что именно нужно делать, а ограничивала задачу, давала только некоторые подходы к ее решению и т. д.
Мы бы очень хотели, чтобы задачи, которые мы даем детям в школе, в большей степени отражали те или иные стороны реальности, готовили их к встрече с жизнью.
Понимание того, что бывают задачи, которые не сумеешь решить ты сам, может быть, и никто в классе, даже учитель и вообще никто, является важным жизненным знанием. Однако, чтобы получить такое представление, надо столкнуться с этим на практике. Это столкновение и содержит зерно истины.